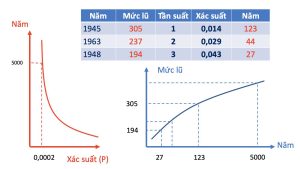
“𝐂𝐨̣̂𝐭 đ𝐢𝐞̣̂𝐧 𝐫𝐨̛̀𝐢 𝐌𝐲̃” 𝐥𝐚̀ 𝐒𝐭𝐭 𝐜𝐮̉𝐚 𝐦𝐨̣̂𝐭 𝐧𝐡𝐚̀ 𝐛𝐚́𝐨, 𝐜𝐡𝐢̣ 𝐯𝐢𝐞̂́𝐭 𝐯𝐞̂̀ 𝐓𝐨̂𝐧 𝐓𝐮𝐧𝐠 (𝐭𝐞̂𝐧 𝐭𝐢𝐞̂́𝐧𝐠 𝐀𝐧𝐡 𝐥𝐚̀ 𝐒𝐮𝐧 𝐒𝐨𝐧𝐠), 𝟑𝟔 𝐭𝐮𝐨̂̉𝐢, 𝐧𝐠𝐮̛𝐨̛̀𝐢 𝐀𝐧 𝐇𝐮𝐲 (𝐓𝐫𝐮𝐧𝐠 𝐐𝐮𝐨̂́𝐜), 𝐥𝐚̀ 𝐠𝐢𝐚́𝐨 𝐬𝐮̛ 𝐭𝐚̣𝐢 Đ𝐚̣𝐢 𝐡𝐨̣𝐜 𝐔𝐂 𝐁𝐞𝐫𝐤𝐞𝐥𝐞𝐲 (𝐇𝐨𝐚 𝐊𝐲̀), đ𝐮̛𝐨̛̣𝐜 𝐝𝐮̛̣ đ𝐨𝐚́𝐧 𝐥𝐚̀ 𝐮̛́𝐧𝐠 𝐯𝐢𝐞̂𝐧 𝐧𝐚̣̆𝐧𝐠 𝐤𝐢́ 𝐧𝐡𝐚̂́𝐭 𝐜𝐡𝐨 𝐇𝐮𝐲 𝐜𝐡𝐮̛𝐨̛𝐧𝐠 𝐅𝐢𝐞𝐥𝐝𝐬 𝐭𝐨𝐚́𝐧 𝐡𝐨̣𝐜 𝟐𝟎𝟐𝟔, 𝐭𝐮̛𝐨̛𝐧𝐠 đ𝐮̛𝐨̛𝐧𝐠 𝐯𝐨̛́𝐢 𝐠𝐢𝐚̉𝐢 “𝐍𝐨𝐛𝐞𝐥 𝐓𝐨𝐚́𝐧 𝐡𝐨̣𝐜”. 𝐃𝐨 𝐜𝐡𝐢́𝐧𝐡 𝐬𝐚́𝐜𝐡 𝐪𝐮𝐨̂́𝐜 𝐭𝐢̣𝐜𝐡, 𝐒𝐮𝐧 𝐜𝐮̀𝐧𝐠 𝐧𝐡𝐢𝐞̂̀𝐮 𝐧𝐡𝐚̀ 𝐤𝐡𝐨𝐚 𝐡𝐨̣𝐜 𝐨̛̉ 𝐌𝐲̃ 𝐯𝐚̀ 𝐜𝐡𝐚̂𝐮 𝐀̂𝐮, đ𝐚̃ 𝐭𝐫𝐨̛̉ 𝐯𝐞̂̀ 𝐓𝐫𝐮𝐧𝐠 𝐐𝐮𝐨̂́𝐜.
Sáng Chủ nhật đọc thông tin này, tôi xin nói tóm tắt về những đóng góp của Sun, gồm một loạt đột phá trong hình học vi phân phức tạp, bao gồm cả sự tồn tại của “Kähler–Einstein metric”, tôi dịch là “Phép đo Kähler-Einstein”.
Phép đo Kähler-Einstein là gì?
Đo lường là một khái niệm cơ bản trong hình học, về bản chất, đo lường liên quan đến tính di động của các hình hình học.
Đầu tiên, tôi giải thích một chút về hình học, nói nôm na mánh qué thì hình học là vật chất. Ví dụ bạn là hình học, tôi cũng là hình học, tôi và bạn có sự giống nhau nhưng cũng có vô vàn thứ khác nhau, cơ thể chúng ta đều được tạo nên từ các tế bào, tế bào được tạo nên từ các nguyên tố hoá học, nguyên tố hoá học được tạo nên từ các nguyên tử, nguyên tử được tạo nên từ các hạt electeron, neutron và proton, các hạt được tạo từ cái gì đó nữa chẳng hạn thì chúng ta không biết. Vì thế mà Heisenberg đặt ra câu hỏi: Thành phần nhỏ nhất của vật chất là gì? Engels đã nói trong tác phẩm ‘Chống Dühring’ rằng: “Các khái niệm về số và hình dạng không bắt nguồn từ bất kỳ nơi nào khác, mà từ thế giới thực, Đối tượng của toán học thuần túy là các dạng không gian và các mối quan hệ định lượng của thế giới thực. Toán học – môn khoa học nghiên cứu các dạng không gian và các mối quan hệ định lượng trong thế giới thực.” Và theo Engels, toán học nói chung và hình học nói riêng, là sản phẩm của tư duy trừu tượng trong thế giới thực.
Vậy thế giới thực đó là gì?
Nếu nhìn trực quan bằng mắt, thì sẽ thấy bạn, thấy tôi, hình ảnh của tôi và bạn mà ai đó quan sát được đó là không gian 3 chiều. Thế nhưng bạn và tôi luôn cử động, dù có im lặng đến thế nào thì vẫn cứ phải thở, tim vẫn đập, máu vẫn chảy, vân vân và mây mây. Sáng ra đo chiều cao của bạn 168cm nhưng chiều đo chỉ còn 167cm vì cột sống buổi chiều lún xuống so với buổi sáng. Cân nặng buổi sáng 57kg, nhưng buổi chiều bạn chỉ còn 56kg do đi lại nhiều toát mồ hôi và ít uống nước, nên cân giảm đi. Như vậy, bạn và tôi luôn thay đổi theo thời gian, vậy thời gian được coi là một chiều, hay chiều thứ tư; tức là thế giới thực đến đây chúng ta tạm hiểu có 4 chiều, gồm 3 chiều không gian và 1 chiều thời gian, được Einstein hay các nhà khoa học gọi là “không – thời gian”. Có nghĩa là vật chất luôn chuyển động theo thời gian. Vậy định dạng hình học của vật chất luôn thay đổi theo thời gian. Tức là thế giới thực không có gì đứng yên. Engels đã nói: ” Chuyển động là phương thức tồn tại của vật chất. Dù khi nào, ở đâu cũng có và không thể có vật chất nếu không có chuyển động.”
Tạm tóm lại, hình học là vật chất, vật chất mà chúng ta nhận thức được là trong không gian 4 chiều, gọi là “không – thời gian”.
Nhưng lí thuyết siêu dây chỉ ra rằng, thế giới chúng ta đang sống, có hẳn 10 chiều.
Giải thích 6 chiều còn lại thì quá dài dòng, nên tạm chấp nhận rằng thế giới này có hẳn 10 chiều chứ không phải chỉ có 4 chiều, theo quan điểm của tôi thì thế giới có thể ít hơn 10 chiều hay nhiều hơn 10 chiều, nhưng về cơ bản trong nhận thức trừu tượng của hình học thì là 10 chiều.
Để nhận thức được vật chất thì chúng ta phải đo lường.
Những kiến thức về đo lường mà chúng ta đang có trong đầu, đó là tư tưởng toán học cổ đại do Euclid đề xuất, phép đo của Euclid là chồng lên nhau. Tức là muốn đo vật chất A so với vật chất B, thì Euclid chọn cách chồng A lên B, nếu vừa khít thì là bằng nhau, nếu không vừa khít thì là không bằng nhau, và như vậy sẽ có 3 khả năng của phép đo.
– Nếu A < B thì A – B < 0
– Nếu A = B thì A – B = 0
– Nếu A > B thì A – B > 0
Đó là phép đo Euclid, nhưng đã bị nhà triết học Schopenhauer chỉ trích vào năm 1844, ông cho rằng nếu các hình chồng lên nhau tự nhiên bằng nhau hoặc giống hệt nhau, sự trùng hợp hoàn toàn là vấn đề mang tính chất thực nghiệm, không thuộc về kiến thức trực quan thuần túy mà thuộc về trải nghiệm giác quan bên ngoài. Schopenhauer cũng chỉ ra rằng, vật chất có hình ảnh luôn chuyển động, và sự di chuyển trong không gian đó nằm ngoài phạm vi của hình học Euclid.
Vào thế kỷ 19, người ta thường thừa nhận rằng để đo kích thước hình học, phải dùng phương pháp xếp chồng hoặc dựa trên một số tiên đề không xác định, hoặc thay vào đó phải sử dụng một phương pháp khác để khám phá sự phù hợp.
Chính vì thế, vào năm 1916 để giải quyết bài toán trường hấp dẫn trong thuyết tương đối rộng, Einstein đã phải sử dụng một cách đo lường khác, đó là lí do ra đời “Phép đo Kähler-Einstein”.
Hiểu về chữ “matric” như thế nào cho đúng?
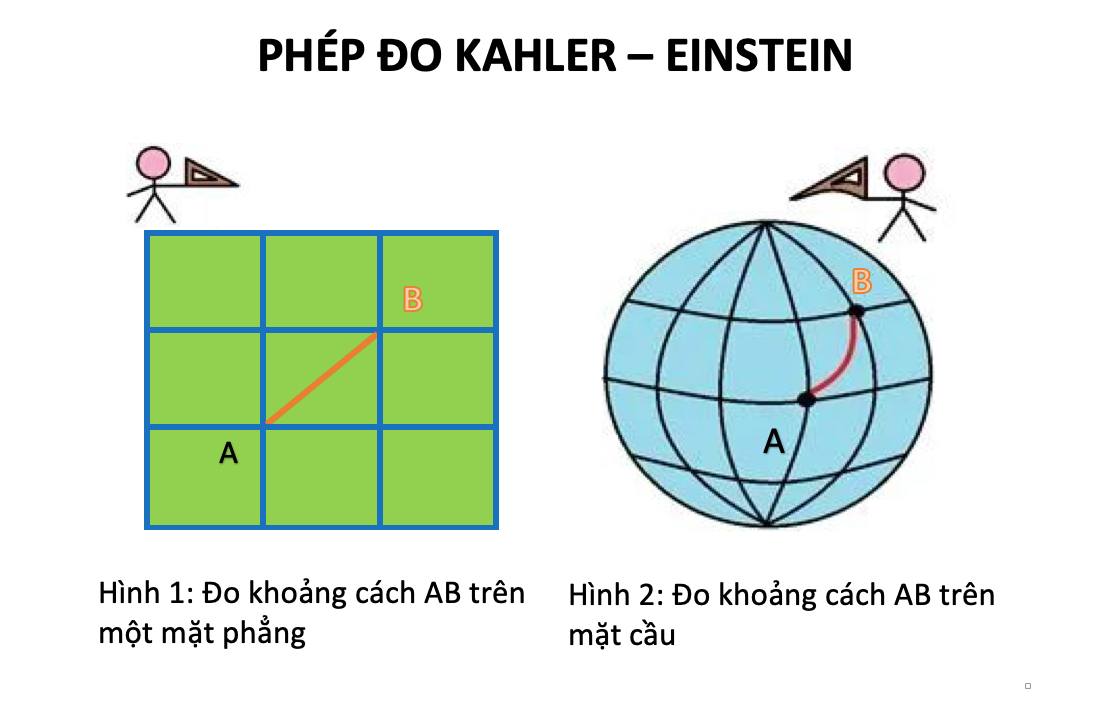
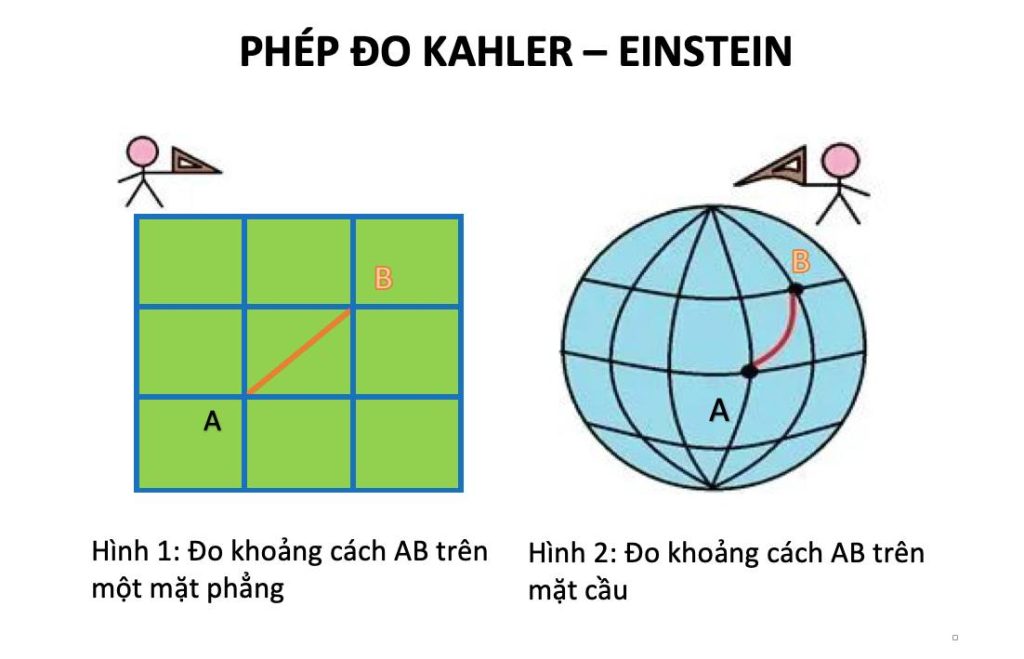
Hình học, tiếng Anh là “geometry”, có nghĩa là trắc địa. Hiểu đơn giản bằng một ví dụ cụ thể, là phép đo khoảng cách từ chỗ tôi đang đứng ở Hà Nội gọi là điểm A, đến chỗ nhà toán học Sun đang đứng ở Bắc Kinh gọi là điểm B. Nếu chỉ dừng ở hình học Euclid, thì phép đo ấy là Hình 1 trong ảnh tôi minh hoạ, tức là dùng eke thẳng để đo. Nhưng trong hình không gian, tức là đo trên mặt quả địa cầu, thì phải dùng eke cong để đo, như Hình 2 tôi minh hoạ ở bên phải. Như vậy, eke thẳng khác với eke cong, tức là hai thước đo có sự khác nhau.
Các thước đo khác nhau ấy chính là “metric”.
Như vậy, metric là quy tắc đo lường, là các phép đo, là các cách thức đo. Vốn liếng tiếng Việt của tôi quá ít, không biết dùng từ nào để dịch “matric”, nên tạm dịch là “Phép đo”, nhờ bạn đọc thông thái chỉ bảo giúp. Và tôi xin được tiếp tục. Một cạnh thẳng và một thước cong là hai loại số liệu khác nhau, trong toán học được biểu diễn bằng một ‘tenxơ số liệu’. Số liệu là các đại lượng hình học và vật lí cơ bản của thuyết tương đối rộng. Các biện pháp đo khác nhau ấy là gì, làm sao thống nhất được nó, luôn là một câu hỏi được đặt ra kể từ khi nhà triết học Schopenhauer chỉ trích Euclid, hay thuyết tương đối rộng của Einstein ra đời. Bởi vì, tất cả những thứ có thể uốn cong (tổng quát hơn là di chuyển hoặc thay đổi như Engels đã chỉ ra) đều là vật chất.
Phải trả lời được câu hỏi của Heisenberg, rằng vật chất nhỏ nhất là gì, thì bài toán “Phép đo Kähler-Einstein” mới giải quyết được triệt để. Thật may mắn, thuyết vướng víu lượng tử đạt giải Nobel 2022, đã mở ra ánh sáng cuối đường hầm.
Điều rất quan trọng là, Marx và Engels đã chỉ ra rằng, chỉ có một vũ trụ vật chất. Bởi nếu có nhiều vũ trụ vật chất, thì chúng ta không thể giải quyết được bài toán “Phép đo Kähler-Einstein”.
Trên thực tế, eke thẳng hay eke cong mà tôi ví dụ, là một chiếc “thước kẻ”. Nếu “thước kẻ” này được kéo thẳng theo kinh nghiệm thành một đường thẳng (cạnh thẳng), thì có thể thu được chiều dài (hoặc khoảng cách cong nếu uốn) của nó. Cạnh thẳng và thước cong ở đây là hai dạng hoặc trạng thái của cùng một thước, tức là cùng độ dài, nhưng lại khác chuyển động (thay đổi).
Do đó, số liệu trong thuyết tương đối rộng là một khái niệm hình học mang tính suy đoán thuần túy, là một quy tắc đo lường sai lầm, không thể phản ánh những thay đổi trong chuyển động của vũ trụ thực.
Theo quan điểm triết học suy đoán, một triết lí cố gắng suy luận hiện thực từ các khái niệm và làm cho sự phát triển của thế giới khách quan phù hợp với những quy luật chung do tư duy con người xây dựng. Và theo suy đoán như vậy, thì “chỉ có một vũ trụ” nên không có thế giới khác bên ngoài vật chất của vũ trụ, không có hình học không – thời gian nào khác ngoài sự phân bố của vật chất trong vũ trụ. Vì vậy, cái gọi là “mô hình vũ trụ học nói chung được chia thành hai phần: Một là hình học không – thời gian; Hai là phân bố vật chất chỉ có thể được mô tả bằng cùng một quy tắc đo lường.
Nếu chỉ dừng ở hiểu biết sơ đẳng của toán học phổ thông, tức là phép đo Euclid có từ thời cổ đại, thì một thước đo chỉ có thể là quy tắc cho phép đo của chính nó, ví dụ đo độ dài dùng thước kẻ, đo trọng lượng dùng cái cân. Và như vậy sẽ có nhiều sai lầm. Ví dụ như, nếu dùng bước chân để đo khoảng cách từ chỗ tôi đứng ở Hà Nội cho đến chỗ nhà toán học Sun đang ở Bắc Kinh, thì bước chân tôi do có nhiều thời gian thảnh thơi hơn nên đi thong dong phải đi 9 triệu bước, trong khi nhà toán học Sun ít thời gian đi vội vã hơn nên sải chân dài hơn thì mất 6 triệu bước.
Hình học không – thời gian của mô hình vũ trụ chỉ là thể hiện sự phân bố vật chất trong chính vũ trụ, vũ trụ ấy chỉ có một, vật chất được hiểu trong vướng víu lượng tử, khi đó mới giải quyết được bài toán “Phép đo Kähler – Einstein”.
Sun giải quyết bài toán ấy như thế nào?
Là một cường quốc toán học, Trung Quốc đang hi vọng sẽ giành được Huy chương Fields 2026, người xứng đáng sẽ là Tôn Tung, hay Sun Song.
Đúng 2500 năm trước, triết gia Heraclitus nhận thấy vạn vật trong thế giới luôn thay đổi, luôn vận động không ngừng, nên ông đã phát biểu một câu nổi tiếng “Không ai có thể tắm hai lần trên một dòng sông”.
Nhưng chỉ đến khi nhà toán học người Nga Aleksandr Friedmann bắt đầu sử dụng các phương trình trường của Einstein để xây dựng mô hình vũ trụ của riêng mình vào năm 1917, thì chúng ta mới ý thức được rõ ràng rằng, vũ trụ học mà Friedmann đã chỉ ra là một quá trình tiến hóa liên tục, thay vì tồn tại đứng yên mãi mãi, tức là trong thế giới này không có gì bất động.
Làm thế nào để thống nhất được phép đo là câu hỏi cực khó.
Muốn thống nhất được, như tôi đã nói ở trên, phải trả lời câu hỏi của Heisenberg – Thành phần nhỏ nhất của vật chất là gì?
Trên thực tế, từ kinh nghiệm của các thí nghiệm khoa học, đường thẳng (chiều dài) là hình dạng hoặc dạng đơn giản và cơ bản nhất trong hình học để mô tả vật chất, tức là thang đo đơn giản và cơ bản nhất để mô tả vật chất. Điểm không phải là một hình dạng cơ bản mô tả vật chất trong hình học, bởi vì điểm được định nghĩa là một thứ không có kích thước hay bộ phận. Trong lịch sử hình học, chưa ai từng chứng minh được rằng một vật không có kích thước hay bộ phận hiện hữu. Chúng ta hãy nhớ lại kiến thức phổ thông về tập đầu tiên của “Các phần tử của hình học”: Điểm là ranh giới của đường thẳng, đường thẳng là ranh giới của các bề mặt, bề mặt là ranh giới của vật thể và vật thể.
Heisenberg cho biết: “Trong 2.500 năm, các triết gia và nhà khoa học tự nhiên đã thảo luận về câu hỏi điều gì sẽ xảy ra nếu người ta tiếp tục phân chia vật chất [về mặt hình học] nhiều lần? Thành phần nhỏ nhất của vật chất là gì? Các triết gia khác nhau đã đưa ra những kết quả rất khác nhau cho câu trả lời cho câu hỏi này, mọi câu trả lời đều có tác động đến lịch sử khoa học tự nhiên.”
Thành tựu vĩ đại nhất của vật lí trong thế kỉ 20 là sự phát triển của vật lí lượng tử. Vật lí lượng tử chỉ ra rằng hầu hết những thay đổi về đại lượng vật lí của các vật thể vi mô đều có những điểm gián đoạn cơ bản, tức là một số đại lượng vật lí nhất định chỉ có thể là bội số của lượng vết nhỏ nhất của chúng, đó là ‘lượng tử’, nghĩa là lượng tử là thành phần nhỏ nhất của vật chất.
Vậy các nhà toán học yên tâm giải quyết bài toán “Phép đo Kähler-Einstein”.
Trung Quốc và các nhà toán học gốc Trung Quốc đi đầu trong giải quyết bài toán này, đầu tiên là việc khám phá ra hệ số K, sau đó từ hình học vi phân đã chứng minh thành công với phép đo có hệ số K âm và bằng không. Nhưng với hệ số K dương thì quá khó, các nhà toán học bắt đầu bối rối.
Tôn Tung đã có những bước đột phá lớn với hệ số K dương, khi giải quyết được “Phép đo Kähler-Einstein”, thì có nghĩa là phép đo trong vũ trụ đã được thống nhất, mà khi đã thống nhất được rồi thì đó là cơ sở để tạo ra rất nhiều những thành tựu khoa học không tưởng trong tương lai.
Đó là lí do Tôn Tung xứng đáng nhận Huy chương Feilds!./.