𝐇𝐢𝐞̂̉𝐮 đ𝐮́𝐧𝐠 𝐤𝐡𝐚́𝐢 𝐧𝐢𝐞̣̂𝐦 𝐥𝐮̃: 𝟏𝟎 𝐧𝐚̆𝐦 𝐦𝐨̣̂𝐭 𝐥𝐚̂̀𝐧, 𝟏𝟎𝟎 𝐧𝐚̆𝐦 𝐦𝐨̣̂𝐭 𝐥𝐚̂̀𝐧, 𝟏𝟎𝟎𝟎 𝐧𝐚̆𝐦 𝐦𝐨̣̂𝐭 𝐥𝐚̂̀𝐧, 𝟓𝟎𝟎𝟎 𝐧𝐚̆𝐦 𝐦𝐨̣̂𝐭 𝐥𝐚̂̀𝐧…”

24/7, báo chí đưa tin UBND tỉnh Nghệ An phát thông báo khẩn, lưu lượng nước về hồ Bản Vẽ đạt 9543 m3/giây, gần mức 5000 năm xảy ra một lần.

Nhiều Fber chửi nhà báo ngu.

Sở dĩ các Fber chửi nhà báo, là vì họ liên tưởng đến lịch sử đất nước chúng ta chỉ có 4000 năm, nên các Fber cho rằng chẳng ai ghi chép được 5000 năm để có được cái gọi là “5000 năm một lần”.

Thực ra đây là một khái niệm trong khoa học thuỷ văn, được các quốc gia trên thế giới dùng để mô tả một trận mưa hoặc một trận lũ xảy ra 1 lần trong N năm nhất định, ở một khu vực nhất định. Và khi đó, 1/N được hiểu là xác suất xảy ra một trận mưa hay trận lũ trong N năm, tức là chỉ cần nghịch đảo xác suất ra số năm N.

N = 5; 10; 15; 20; 25… 5000 năm và nhiều vô tận.

Và N = 5000 năm thì xác suất sẽ là 1:5000 = 0,0002 = 0,02%

Tôi hoàn toàn thông cảm với mọi người, bởi nếu không có những kiến thức toán thống kê cơ bản, thì đọc những thuật ngữ này sẽ rất bối rối dẫn tới chửi lung tung.

Để tôi lấy cho bạn một ví dụ.

Giả sử chúng ta muốn xây một cây cầu bắc qua sông. Trong số rất nhiều vấn đề thiết kế, có một câu hỏi: nên xây cầu cao bao nhiêu? Như chúng ta đã biết, mực nước sông không phải lúc nào cũng ổn định, nó sẽ lên xuống thất thường. Nếu chúng ta xây cầu vào mùa đông, cầu có thể bị lũ cuốn trôi vào mùa hè. Một số người có thể nói rằng chúng ta nên xây cầu càng cao càng tốt. Nhưng xây cao quá sẽ lãng phí, rồi ai đó leo lên Facebook sẽ chửi chúng ta là lãng phí tiền thuế của họ, cứ chửi thôi dù có thể người chửi chẳng đóng góp được bao nhiêu thuế. Vì vậy, chúng ta cần xác định chiều cao của cầu một cách khoa học, để không lãng phí kinh phí xây dựng cầu và đảm bảo an toàn cho cây cầu.

Chúng ta mời một chuyên gia về thủy văn và tính toán lũ.

Vị chuyên gia hỏi: “Các anh muốn thiết kế cây cầu chịu được lũ lụt trong bao nhiêu năm?” Theo phong cách khiêm tốn của người Việt chúng ta rụt rè trả lời: “5000 năm mới có một lần”. Chuyên gia vỗ đùi nói: “Được rồi để tôi tính.”

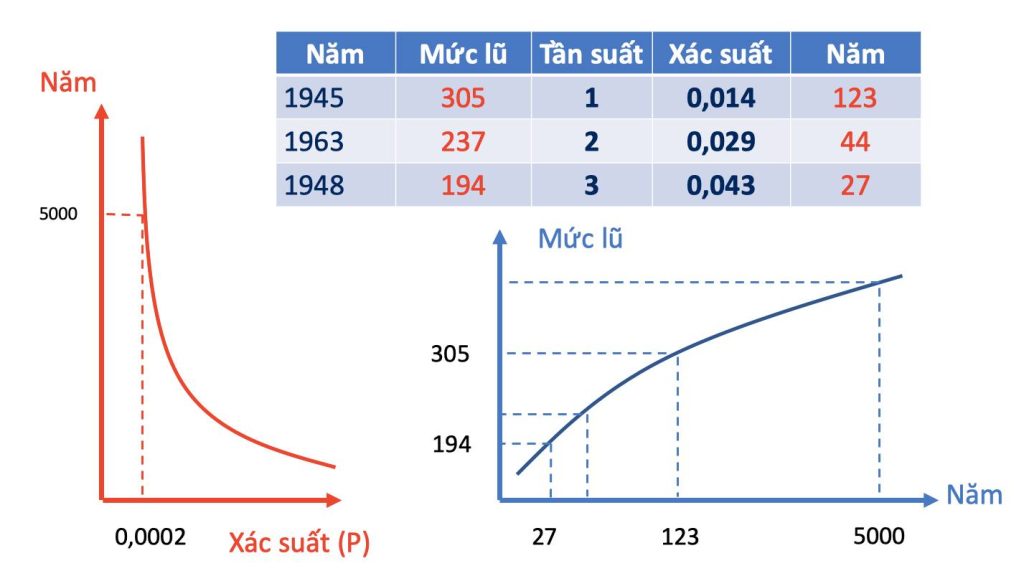
Đầu tiên, chuyên gia vẽ một cái đồ thị, trong đó trục hoành là xác suất xảy ra một trận lũ trong N năm, trục tung là số năm tương ứng với xác suất ấy. Hình minh hoạ là màu xanh. Vị chuyên gia đánh đấu xác suất P = 0,0002 có ngĩa là 2/10000 = 1/5000 như vậy gióng lên trục tung thì ta có con số 5000, thì được hiểu là mức lũ xảy ra với xác suất 5000 năm mới có 1 lần.

Nhưng cụ thể mức lũ ấy là bao nhiêu?

Bây giờ, chuyên gia phải tìm kiếm dữ liệu lũ qua các năm tại lưu vực sông này, số liệu càng nhiều thì tính toán càng chính xác.

Tôi giả sử vị chuyên gia có được dữ liệu, đó là cơ quan thuỷ văn bắt đầu ghi chép về khúc sông đó kể sau Cách mạng Tháng 8, tức là vừa đúng n = 69 năm.

Chuyên gia thuỷ văn bắt đầu tính xác suất.

Năm 1945, lưu lượng chảy lớn nhất 305 m3/s, cũng là mức cao nhất trong 69 năm, vậy xác suất xảy ra là 1/69 = 0,014.

Năm 1963, lưu lượng chảy lớn nhất 194 m3/s, mức cao thứ hai, tức là trong 69 năm có hai lần xảy ra lũ cao hơn hoặc bằng giá trị này, vậy xác suất xảy ra là 2/69 = 0,029.

Năm 1948, lưu lượng chảy lớn nhất 214 m3/s, cũng là mức cao thứ ba, tức là trong 69 năm có ba lần mức lũ cao hơn hoặc bằng giá trị này, vậy xác suất xảy ra là 3/69 = 0,043.

Có một số thuật toán tối ưu trong thống kê nữa, dựa vào dữ liệu để thực hiện điều chỉnh cho ra được con số xác suất chính xác với thực tế hơn, thì tử số giảm nhẹ 0,44 và mẫu số tăng nhẹ 0,12 nhưng vì Facebook không cho đăng thuật toán nên tôi không tiện lí giải. Như vậy sẽ có ba xác suất gồm 0,008 – 0,023 – 0,037. Nghịch đảo xác suất sẽ có năm 123 năm, 44 năm và 27 năm tương ứng.

……………

Cứ như vậy, chuyên gia lập được một cái bảng Excel, sử dụng hai cột màu đỏ tạo được một loạt các điểm trong hệ trục toạ độ màu đỏ. Trong hệ toạ độ này, trục hoành là số năm N, còn trục tung là đỉnh lũ đạt được. Nghĩa là chuyên gia sẽ có một tập hợp các điểm (123; 305), (44, 237), (27; 214)… Đây chính là hàm mật độ trong toán thống kê, tức là lập phương trình đồ thị hàm số đi gần các điểm nhất, chỉ cần kiến thức thống kê cơ bản cũng lập được.

Nhập dữ liệu máy tính có ngay hàm số.

Đến bây giờ thì xong rồi, chúng ta muốn 100 năm, 1000 năm, hay 5000 năm, thậm chí đòi hỏi chuyên gia cung cấp mức lũ với xác suất hàng tỉ năm mới có một lần, thì chuyên gia cũng ngay lập tức đưa cho chúng ta con số.

Những thuật toán thống kê này ứng dụng thực tế rất nhiều, ví dụ tính chiều cao cân nặng, tính BMI cơ thể, tính trọng lượng thai nhi bằng siêu âm.

Mọi người có thể vào đọc các bài trên báo nước ngoài:

1. 6 rare ‘1,000-year’ rain events within a month? Climate change may force NOAA to update criteria

2. A 5000-Year Record of Extreme Floods and Climate Change in the Southwestern United States